COMSOL 5.6破解文件

COMSOL 5.6破解文件是针对同名软件制作的一个激活破解文件，能够帮助用户激活软件的所有功能免费使用，而不需要再花钱去购买。COMSOL 5.6全称也为COMSOL Multiphysics 5.6，是由COMSOL公司出品的一款仿真模拟软件，可以满足用户仿真模拟的所有需求，成为用户的首选仿真工具。该软件在工程、科研、制造、声学、生物科学、化学反应、弥散、电磁学、流体动力学、燃料电池等领域有着广泛的应用，并具有灵活、易用的特点，相比于其他软件的强大之处在于，里面有非常多的扩展功能，模拟效率大大加倍。软件内嵌丰富的CAD建模工具，用户可直接在软件中进行二维和三维建模，同时支持全面的第三方CAD导入功能，支持当前主流CAD软件格式文件的导入。不过该软件目前没有免费版本，不购买的话只能试用，而且功能还有限制，所以小编为你们带来了COMSOL 5.6破解补丁，可有效激活软件免费使用，有需要的朋友欢迎前来下载。

COMSOL 5.6破解文件使用教程

1、在本站下载解压，得到文件内容；

2、首先用安装COMSOL 5.6官方软件；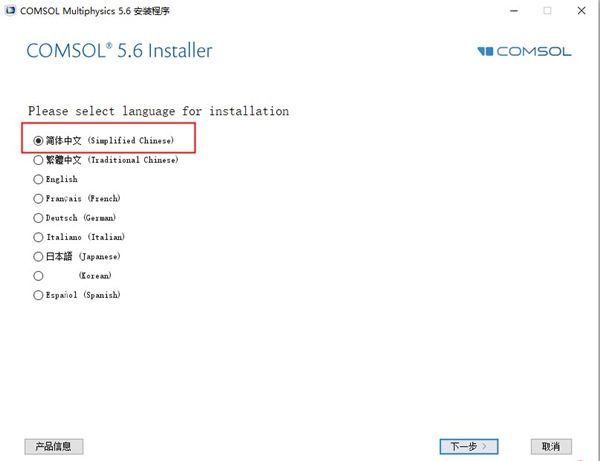

3、选择新安装comsol5.6；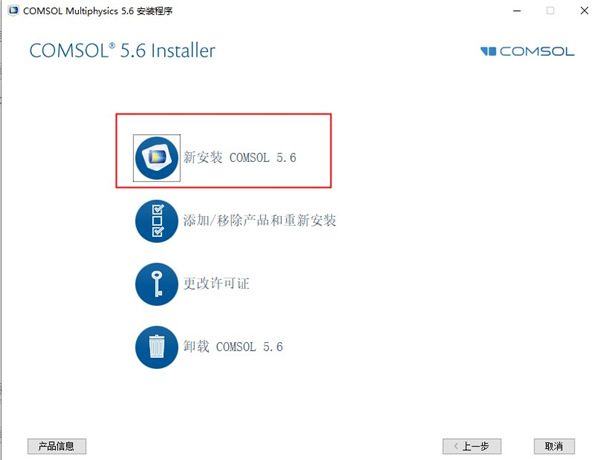

4、接受安装协议，许可证格式选择“许可证文件”，再选择软件包中_SolidSQUAD_文件夹下的“LMCOMSOL_Multiphysics_SSQ.lic”许可证文件；
提示：许可证文件你可以放在一个指定的文件夹，比如直接放在安装目录下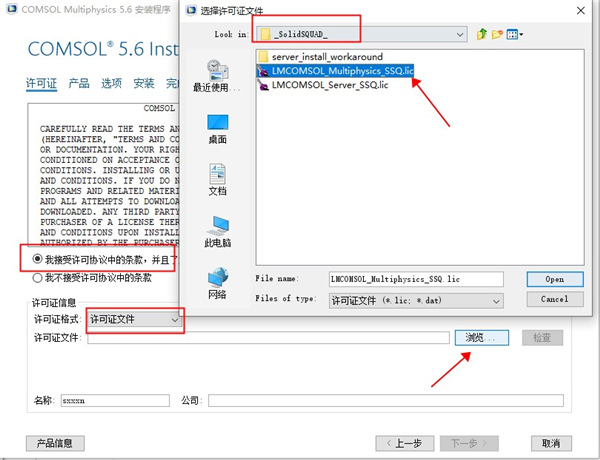

5、选择你要安装的产品和安装目录，默认全部安装；
默认目录【C:\Program Files\COMSOL\COMSOL56\Multiphysics】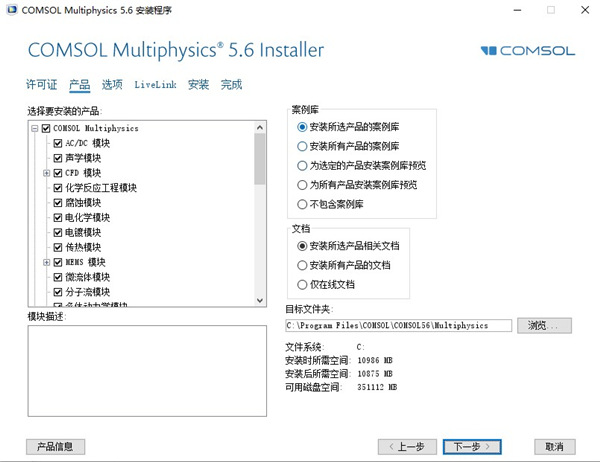

6、在选中，不用勾选安装完成后检查更新”和“启动自动检查更新”；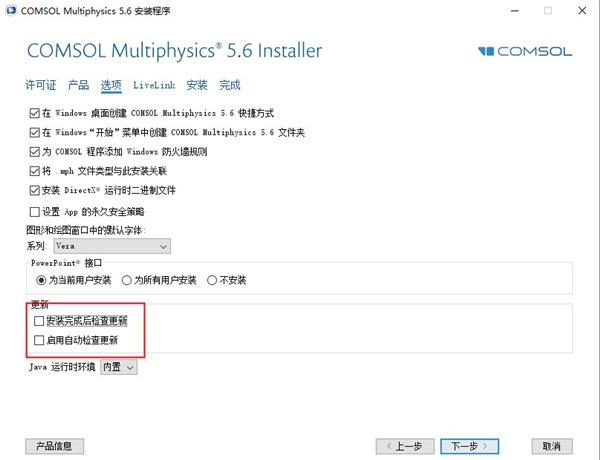

7、依提示进行下一步，开始正式安装软件；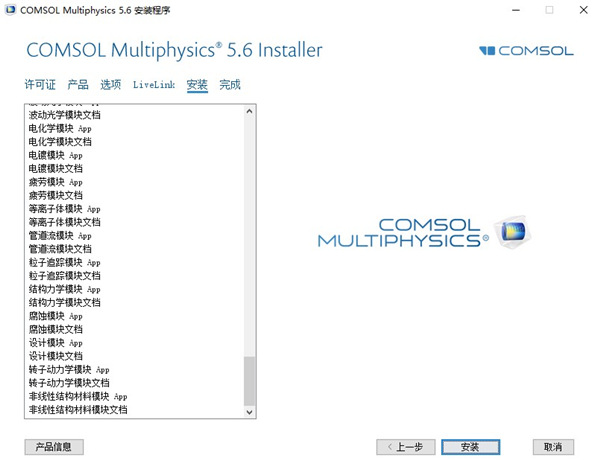

8、软件正在安装中，需要一点时间，请您耐心等待；

9、软件安装成功啦；

10、运行软件，可以看到软件已经破解成功啦，以上就是使用教程。

comsol使用技巧

一、全局约束  
对于多物理仿真，添加全局约束是COMSOL非常有用的功能之一
1.例如，对于一个涉及传热的仿真，希望能够调整热源Q_0的大小，从而使得某一位置处的温度T_probe恒定在指定值T_max，我们可以直接将这个全局约束添加进来即可
2.有些情况下，全局约束可能包含有对时间的微分项，也就是常说的常微分方程（ODE），软件L同样也支持自定义ODE作为全局约束
3.例如，在一个管道内流体+物质扩散问题的仿真中，利用PID算法控制管道入口的流速u_in_ctrl，从而使得某一位置处的浓度conc恒定在指定值c_set。（基本模块模型库 > Multidisciplinary > PID control）
4.要添加上述约束，除变上限积分项外，另外两项都可以很容易的在边界条件中的“入口流速”设置中直接定义。因此，这个变上限积分需要转化成一个ODE，作为全局约束加入
5.令方程两边同对时间t求导，得到 setcconcdt d_int。在COMSOL中，变量u对时间的导数，用ut表示。因此变量int的时间导数即为intt。利用COMSOL的“ODE设定”，我们可以很容易的将intt-(conc-c_set)=0这个ODE全局约束添加入模型之中
二、积分耦合变量
COMSOL的语法中，变量u对空间的微分，分别默认为用ut，ux，uy，uz等来表示，这为仿真提供了极大的便利。那么对变量u的空间积分呢？COMSOL提供了积分耦合变量来实现这一功能
1.积分耦合变量分为四种：点(point)积分耦合变量、边(edge)积分耦合变量、边界(boundary)积分耦合变量、求解域(subdomain)积分耦合变量。根据模型的维度，会有相应积分耦合变量。用户还可以指定得到结果后的作用域，例如全局，或指定某些点、边、边界或求解域。从而可以将对积分耦合变量结果的访问限制在指定的对象上
2.求解域积分耦合变量，就是对指定变量或表达式在指定的某个或者某些求解域上做积分，积分的结果赋给自定义的这个积分耦合变量。对于三维仿真，这个积分是体积分；对于二维则是面积分。最典型的应用当属对数值1进行积分，可以得到体积或面积
3.边界积分耦合变量，就是对指定变量或表示在指定的某个或者某些边界上做积分，积分的结果付给自定义的这个积分耦合变量。对于三维仿真，这个积分是面积分；对于二维则是线积分。对1积分可以得到面积或边长
4.边积分耦合变量，就是对指定变量或表达式在指定的某个或者某些边上做积分，积分的结果付给自定义的这个积分耦合变量。仅存在于三维仿真中，这个积分是线积分。对1积分得到边长
5.点积分耦合变量，就是对指定变量或表达式在指定的某个或者某些点上给出它的值。它的最主要用法是将某个点上的结果映射到指定的对象上
6.在上面PID控制的例子中，指定位置处的浓度conc就是一个点积分耦合变量，用来提取点PT1处的浓度值。同时，浓度c的时间变化率ct在PT1点的取值，也可以用同样的方法提取出来，付给变量ctim
7.积分耦合变量除了用于添加约束，也常常用于后处理。COMSOL允许用户将任意表达式在任意求解域或者边界上的积分定义为一个变量，然后直接在后处理中对该自定义的积分耦合变量做数据可视化操作
8.例如，在二维扩散问题的仿真中，为了观测流出边界上总的流出的物质量，可以在出口边界利用边界耦合积分变量，然后可以直接得到数据曲线。（基本模块模型库 > Chemical engineering > absorption）
三、非线性特征值问题
1.求解方程的特征值是仿真中经常碰到的一类问题。问题线性度比较好的时候，方程的系数与方程的解变量u不存在函数关系，这样的方程很容易解；反过来，方程特征值也很容易求。但是有时候我们会碰到非线性比较强的问题，方程的系数本身就是解变量u的函数。对于正问题，COMSOL很容易“求解域设定”中，定义方程的某些系数是解变量的函数，然后利用软件提供的非线性求解器完成求解。但是对于非线性很强的逆问题又该如何定义呢？这里有一个很好用的技巧，就是使用全局约束对特征值先进行一下归一化，在这里定义特征值与解变量相关。
2.例如PDE方程即为特征值（下图中的Lambda）。我们可以先添加全局约束，定义E=1，而E其实是一个积分耦合变量，对应于解变量u2在求解域上的积分。通过这样操作，我们就把Lambda和解变量u建立的联系，然后使用软件提供的非线性求解器完成求解